1.1 Definisi Integral Tak Tentu (Indefinite Integral)
mempunyai suku konstanta sembarang.
1.2 Rumus-rumus Integral Tak Tentu
1.3 Definisi Integral Tentu
sebagai berikut:
maka menurut dalil pokok dari kalkulus integral, integral tentu diatas dapat dihitung dengan
rumus :
1.4 Rumus-rumus Integral tentu
- Salah satunya dimisalkan U
- Sisinya yang lain (termasuk dx) dianggap sebagai dv
1.6 Beberapa Aplikasi dari Integral
a. Perhitungan Luas suatu kurva terhadap sumbu x




b. Menghitung luas diantara dua buah kurva

c. Menghitung volume benda putar yang diputar terhadap sumbu koordinat







b. Menghitung luas diantara dua buah kurva

c. Menghitung volume benda putar yang diputar terhadap sumbu koordinat



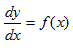
















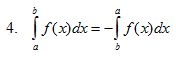



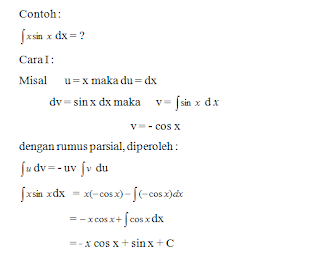
















0 komentar:
Posting Komentar