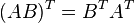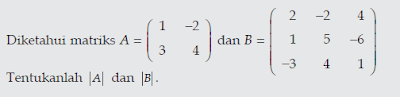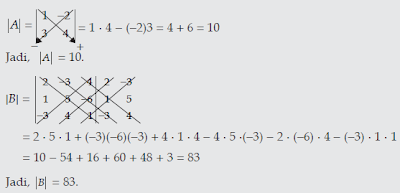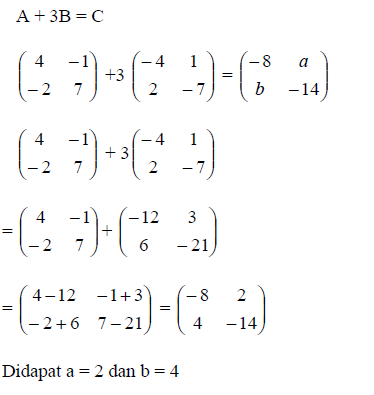2013 ~ Mat Eko_Stat Eko & Metrik

28 Agustus 2013

JENIS-JENIS MATRIKS

7:49:00 AM MATERI MATEMATIKA EKONOMI 2 (MATRIKS) No comments

Jenis-jenis matriks dapat dibagi berdasarkan ordo dan elemen / unsur dari matriks tersebut.

Berdasarkan ordo Matriks dapat di bagi menjadi beberapa jenis yaitu :

Matriks Bujursangkar adalah matriks yang memiliki ordo n x n atau banyaknya baris sama dengan banyaknya kolom yang terdapat dalam mtriks tersebut. Matriks ini disebut juga dengan matriks persegi berordo n.

Contoh :

Matriks Baris adalah Matriks Baris adalah matriks yang terdiri dari satu baris

Contoh : A = ( 2 1 3 -7 )

Matriks Kolom adalah Matriks Kolom adalah matriks yang terdiri dari satu kolom.

Contoh :

Matriks Tegak adalah suatu matriks yang banyaknya baris lebih dari banyaknya kolom.

Contah :

Matriks datar adalah Matriks yang banyaknya baris kurang dari banyaknya kolom.

Contoh :

Berdasarkan elemen-elemen penyusunnya matriks dapat di bagi menjadi beberapa jenis yaitu :

Matriks Nol adalah Suatu matriks yang setiap unsurnya 0 berordo m x n, ditulis dengan huruf O.

contoh :

Matriks Diagonal adalah suatu matriks bujur sangkar yang semua unsurnya , kecuali unsur-unsur pada diagonal utama adalah nol.

Contah :

Matriks Segi Tiga adalah suatu matriks bujur sangkar yang unsur-unsur dibawah atau diatas diagonal utama semuanya 0 .

Contoh :

Dimana Matriks C disebut matriks segi tiga bawah dan matriks D disebut matriks segitiga atas.

Matriks Skalar adalah matriks diagonal yang unsur-unsur pada diagonal utama semuanya sama.

Contoh :

Matriks Identitas atau Matriks Satuan adalah matriks diagonal yang unsur-unsur pada diagonal utama semuanya satu ditulis dengan huruf I.

Contoh :

Matriks Simetri adalah suatu matriks bujur sangkar yang unsur pada baris ke-i kolom ke-j sama dengan unsur pada baris ke-j kolom ke-i sehingga aij = aji .

Contoh :

JENIS-JENIS MATRIKS

7:32:00 AM MATERI MATEMATIKA EKONOMI 2 (MATRIKS) No comments

TRANSPOS MATRIKS

6:54:00 AM MATERI MATEMATIKA EKONOMI 2 (TRANSPOS MATRIKS 3 x 3 & CONTOH SOAL) No comments

Transpos Matriks

Yang dimaksud dengan Transpos dari suatu matriks adalah mengubah komponen-komponen dalam matriks, dari yang baris menjadi kolom, dan yang kolom di ubah menjadi baris.

Contoh: Matriks

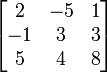A = $\begin{bmatrix} 2 & -5 & 1\\ -1 & 3 & 3\\ 5 & 4 & 8\\ \end{bmatrix}$ ditranspose menjadi A^T = $\begin{bmatrix} 2 & -1 & 5\\ -5 & 3 & 4\\ 1 & 3 & 8\\ \end{bmatrix}$

Matriks

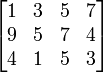B = $\begin{bmatrix} 1 & 3 & 5 & 7\\ 9 & 5 & 7 & 4\\ 4 & 1 & 5 & 3\\ \end{bmatrix}$ ditranspose menjadi B^T = $\begin{bmatrix} 1 & 9 & 4\\ 3 & 5 & 1\\ 5 & 7 & 5\\ 7 & 4 & 3\\ \end{bmatrix}$

Rumus-rumus operasi Transpose sebagai berikut:

1. $((A)^T)^T = A$

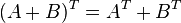2. $(A+B)^T = A^T + B^T$ dan $(A-B)^T = A^T - B^T$

3. $(kA)^T = kA^T$ dimana k adalah skalar

4. $(AB)^T = B^T A^T$

MINOR & KOFAKTOR MATRIKS

6:44:00 AM MATERI MATEMATIKA EKONOMI 2 (MINOR & KOFAKTOR MATRIKS 3 x 3 & CONTOH SOAL) 1 comment

Definisi :

Jika A adalah matriks kuadrat, maka minor a_ij dinyatakan oleh M_ij adalah submatriks A yangdidapat dengan jalan menghilangkan baris ke-i dan kolom ke - j.

Kofaktor a_ij dinyatakan oleh C_ij didefinisikan sebagai: C_ij = (-1)^{I + j}.M_ij.

Determinan suatu matriks kuadrat A dapat juga dihitung dengan menggunanakan ekspansi kofaktor sepanjang baris/kolom.

Berikut ini adalah Contoh Rumus Kofaktor sbb:

Teorema :
Determinan matriks A yang berukuran n x n dapat dihitung dengan mengalikan entri-entri dalam suatu baris (atau kolom) dengan kofaktor-kofaktornya dan menambahkan hasil kali yang dihasilkan, yaitu untuk setiap 1£ i £ n dan 1£ j £ n, maka

Jawab: jika det(A) dihitung menggunakan ekspansi kofaktor sepanjang kolom 1, maka

Definisi :
Jika A sebarang matriks n x n dan Cij adalah kofaktor aij, maka matriks

dinamakan matriks kofaktor A. Transpose matriks ini dinamakan adjoin A ditulis adj(A)

CARA MENGHITUNG INVERS MATRIKS 3 X 3

5:26:00 AM MATERI MATEMATIKA EKONOMI 2 (RUMUS INVERS MATRIKS 3 x 3 & CONTOH SOAL) 1 comment

Contoh Matrix:

1. Cari Adjoint: M disebut sebagai minor.

2. Cari penentu setiap matriks 2x2 kecil.

3. Transpos untuk mendapatkan Adjoint

4. Cari Inverse Dengan Formula ini:

5. Hitung dengan Formula atas dan Invers.

CARA MENGHITUNG ADJOINT MATRIKS 3 X 3

5:15:00 AM MATERI MATEMATIKA EKONOMI 2 (RUMUS ADJOINT MATRIKS 3 x 3 & CONTOH SOAL) No comments

Contoh Matrix:

1. Cari Adjoint: M disebut sebagai minor.

2. Cari penentu setiap matriks 2x2 kecil.

3. Transpos untuk mendapatkan Adjoint

4. Cari Inverse Dengan Formula ini:

5. Hitung dengan Formula atas dan Invers.

CARA MENGHITUNG DETERMINAN MATRIKS 3 X 3

5:09:00 AM MATERI MATEMATIKA EKONOMI 2 (DETERMINAN MATRIKS 3 x 3 (RUMUS & CONTOH SOAL) No comments

Contoh Matriks:

1. Cari Determinan Matriks: Determinan biasanya akan muncul dalam penyebut kebalikannya. Jika determinan adalah nol, matriks tidak akan memiliki invers.

DETERMINAN MATRIKS 3 x 3 (RUMUS & CONTOH SOAL) 1

2:27:00 PM MATERI MATEMATIKA EKONOMI 2 (DETERMINAN MATRIKS 3 x 3 (RUMUS & CONTOH SOAL) No comments

Setiap matriks persegi mempunyai nilai determinan. Nilai determinan dari suatu matriks merupakan suatu skalar. Jika nilai determinan suatu matriks sama dengan nol, maka matriks tersebut disebut matriks singular. Matriks singular tidak mempunyai invers/balikan.

Untuk matriks B berordo 3 x 3, determinan matriks B ini didefinisikan sebagai berikut menggunakan kaidah Sarrus.

Berikut adalah Contoh perhitungan Determinan Matriks 3 x 3 (poin 2):

INVERS MATRIKS 2 x 2 (RUMUS & CONTOH SOAL) 1

1:55:00 PM MATERI MATEMATIKA EKONOMI 2 (RUMUS INVERS MATRIKS 2 x 2 & CONTOH SOAL) No comments

Suatu matriks dapat dibalik jika dan hanya jika matriks tersebut adalah matriks persegi (matriks yang berukuran n x n) dan matriks tersebut non-singular (determinan $\neq$ 0). Tidak semua matriks memiliki invers. Invers matriks dapat didefinisikan sebagai berikut.

Definisi:

Jika A adalah suatu matriks kuadrat, dan jika kita dapat mencari matriks B sehingga AB = BA = I, maka A dikatakan dapat dibalik (invertible) dan B dinamakan invers dari A

Sifat matriks invers:

1. (A^t)^t = A

2. (A + B)^t = A^t + B^t

3. (A . B)^t = B^t . A^t

4. (A^-t)^-t = A

5. (A . B)^-1 = B^-1. A^-1

6. A . B = C ® |A| . |B| = |C|

Sumber Lain:

For a

matrix

(2)

the matrix inverse is

			(3)
			(4)

Contoh 1:

Hitung invers matriks A_2×2 berikut A = $\left [ \begin{array}{rr}3 & 5\\ 1 & 2\end{array} \right ]$ .

Penyelesaian:

Jika kita punya matriks 2×2, misal A = $\left [ \begin{array}{rr}a & b\\ c & d\end{array} \right ]$ , maka invers matriks dapat dihitung menggunakan rumus

A^-1 = B = $\frac{1}{det \quad A}$ $\left [ \begin{array}{rr}d & -b\\ -c & a\end{array} \right ]$

= $\frac{1}{3(2)-5(1)}$ $\left [ \begin{array}{rr}2 & -5\\ -1 & 3\end{array} \right ]$

= $\left [ \begin{array}{rr}2 & -5\\ -1 & 3\end{array} \right ]$

Cek, apakah AB = BA = I

AB = $\left [ \begin{array}{rr}3 & 5\\ 1 & 2\end{array} \right ]$ $\left [ \begin{array}{rr}2 & -5\\ -1 & 3\end{array} \right ]$ = $\left [ \begin{array}{rr}1 & 0\\ 0 & 1\end{array} \right ]$ = I

BA = $\left [ \begin{array}{rr}2 & -5\\ -1 & 3\end{array} \right ]$ $\left [ \begin{array}{rr}3 & 5\\ 1 & 2\end{array} \right ]$ = $\left [ \begin{array}{rr}1 & 0\\ 0 & 1\end{array} \right ]$ = I

Karena AB = BA = I, maka berdasarkan Definisi, B adalah invers dari matriks A.

Bagaimana cara menghitung invers jika matriksnya memiliki ordo lebih dari 2? Misal matriks 3×3, 4×4, dan seterusnya. Pada matriks yang berordo lebih dari dua ini kita akan memanfatkan Eliminasi Gauss Jordan.

Sumber: Anton, H., 1992, Aljabar Linier Elementer, Erlangga, Jakarta.

Contoh soal dari determinan ditunjukkan sebagai berikut: