PANGKAT, AKAR DAN LOGARITMA ~ Mat Eko

24 Agustus 2013

PANGKAT, AKAR DAN LOGARITMA

6:57:00 AM AKAR DAN LOGARITMA), MATERI MATEMATIKA EKONOMI 1 (PANGKAT No comments

Rumus Bentuk Pangkat, Akar, dan Logaritma

a. Bentuk Pangkat
1). Jika n bilangan bulat positif dan a bilangan real maka a pangkat n didefinisikan sebagai berikut :
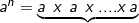
       $\inline \fn_cm a^{n}=\underbrace{a \: \: x \: \: a\:\: x\: ....x\: a}$
      Pengertian pangkat tersebut diperluas, yaitu untuk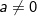 $\inline \fn_cm a\neq 0$ berlaku :
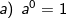
       $\inline \fn_cm a)\: \: a^{0}=1$
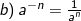
       $\inline \fn_cm b)\: a^{-n}=\frac{1}{a^{n}}$
2). Sifat-sifat pengerjaan hitung bilangan berpangkat
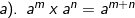
       $\inline \fn_cm a).\: \: a^{m}\: x\: a^{n}=a^{m+n}$
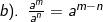
       $\inline \fn_cm b).\: \: \frac{a^{m}}{a^{n}}=a^{m-n}$
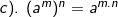
       $\inline \fn_cm c).\: \: (a^{m})^{n}=a^{m.n}$
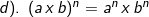
       $\inline \fn_cm d).\: \: (a\, x\, b)^{n}=a^{n}\, x\, b^{n}$
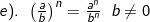
       $\inline \fn_cm e).\: \: \left ( \frac{a}{b} \right )^{n}=\frac{a^{n}}{b^{n}}\, \, \: b\neq 0$

b. Bentuk Akar
1). Jika a dan b bilangan real serta n bilangan bulat positif, maka :
       $\inline \fn_cm a).\: \: b^{n}=a\, \Leftrightarrow \, \sqrt[n]{a}=b$
       $\inline \fn_cm b).\: \: \sqrt[n]{a}=a^{\frac{1}{n}}$
2). Sifat-sifat bentuk akar.
       $\inline \fn_cm a).\: \: \sqrt[n]{a^{m}}=a^{\frac{m}{n}}$
       $\inline \fn_cm b).\: \: p\sqrt[n]{a}+q\sqrt[n]{a}=(p+q)\sqrt[n]{a}$
       $\inline \fn_cm c).\: \: p\sqrt[n]{a}-q\sqrt[n]{a}=(p-q)\sqrt[n]{a}$
       $\inline \fn_cm d).\: \: \sqrt[n]{a.b}=\sqrt[n]{a}\,\, x\, \sqrt[n]{b}$
       $\inline \fn_cm e).\: \: \sqrt[n]{\frac{a}{b}}=\frac{\sqrt[n]{a}}{\sqrt[n]{b}}\, ,b\neq \neq 0$
       $\inline \fn_cm f).\: \: \sqrt[m]{\sqrt[n]{a}}=\sqrt[m.n]{a}$
3). Merasionalkan penyebut pecahan bentuk akar
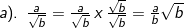
       $\inline \fn_cm a).\: \: \frac{a}{\sqrt{b}}=\frac{a}{\sqrt{b}}\, x\, \frac{\sqrt{b}}{\sqrt{b}}=\frac{a}{b}\sqrt{b}$
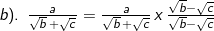
       $\inline \fn_cm b).\: \: \frac{a}{\sqrt{b}\, +\sqrt{c}}=\frac{a}{\sqrt{b}\, +\sqrt{c}}\, x\, \frac{\sqrt{b}-\sqrt{c}}{\sqrt{b}-\sqrt{c}}$
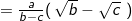
                            $\inline \fn_cm =\frac{a}{b-c}(\, \sqrt{b}-\sqrt{c}\, \, )$

c. Logaritma
1). Jika a dan b bilangan positif dengan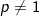 $\inline \fn_cm p\neq 1$ maka berlaku :
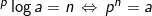
       $\inline \fn_cm {}^{p}\log{a}=n\, \Leftrightarrow \, p^{n}=a$
      Dari hubungan tersebut, diperoleh :
       $\inline \fn_cm a).\, \, p^{0}=1\, \Leftrightarrow \, {}^{p}\log{1}=0$
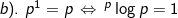
       $\inline \fn_cm b).\, \, p^{1}=p\, \Leftrightarrow \, {}^{p}\log{p}=1$
       $\inline \fn_cm c).\, \, p^{n}=p^{n}\, \Leftrightarrow \, {}^{p}\log{p^{n}}=n$
2). Sifat-sifat logaritma
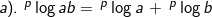
       $\inline \fn_cm a).\, \, {}^{p}\log{ab}=\, {}^{p}\log{a}\, +\, {}^{p}\log{b}$
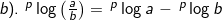
       $\inline \fn_cm b).\, \, {}^{p}\log{\left ( \frac{a}{b} \right )}=\, {}^{p}\log{a}\, -\, {}^{p}\log{b}$
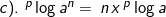
       $\inline \fn_cm c).\, \, {}^{p}\log{a^{n}}=\, n\, x\, {}^{p}\log{a}$
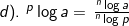
       $\inline \fn_cm d).\, \, {}^{p}\log{a}=\, \frac{{}^{n}\log{a}}{{}^{n}\log{p}}$
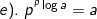
       $\inline \fn_cm e).\, \, p^{{}^{p}\log{a}}=a$

Mat Eko_Stat Eko & Metrik

24 Agustus 2013