INVERS MATRIKS 3 x 3 (RUMUS & CONTOH SOAL) 1 ~ Mat Eko

27 Agustus 2013

INVERS MATRIKS 3 x 3 (RUMUS & CONTOH SOAL) 1

1:35:00 PM MATERI MATEMATIKA EKONOMI 2 (RUMUS INVERS MATRIKS 3 x 3 & CONTOH SOAL) No comments

Inverse matrix of 3

There exists an inverse matrix of A when detA = a₁₁a₂₂a₃₃ + a₂₁a₃₂a₁₃+ a₃₁a₁₂a₂₃- a₁₁a₃₂a₂₃- a₃₁a₂₂a₁₃- a₂₁a₁₂a₃₃

0, and it is

Sumber lain:

For a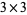

matrix

(5)

the matrix inverse is

A^(-1)=1/(|A|)[|a_(22) a_(23); a_(32) a_(33)| |a_(13) a_(12); a_(33) a_(32)| |a_(12) a_(13); a_(22) a_(23)|; ; |a_(23) a_(21); a_(33) a_(31)| |a_(11) a_(13); a_(31) a_(33)| |a_(13) a_(11); a_(23) a_(21)|; ; |a_(21) a_(22); a_(31) a_(32)| |a_(12) a_(11); a_(32) a_(31)| |a_(11) a_(12); a_(21) a_(22)|].

Contoh 1:

Carilah invers matriks 3×3 yaitu A = $\left [\begin{array}{rrr} 1& 2& 3\\ 2& 5& 3\\ 1& 0& 8 \end{array} \right ]$

Penyelesaian:

Susun matriks sedemikian sehingga seperti dibawah ini.

$\left[ \left.\begin{matrix} 1& 2& 3\\ 2& 5& 3\\ 1& 0& 8 \end{matrix}\right| \begin {array}{rrr} 1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end {array}\right]$

Matriks disebelah kiri adalah matriks A dan sebelah kanan adalah matriks identitas. Kemudian lakukan Operasi Baris Elementer sedemikan sehingga matriks sebelah kiri menjadi matriks identitas dan matriks identitas (pada sebelah kanan) yang akan menjadi invers matriks tersebut.

baris kedua: B₂ + (-2B₁) [artinya baris kedua dijumlahkan dengan -2 kali baris pertama]

baris ketiga : B₃ + (-B₁) [artinya baris kedua dijumlahkan dengan -1 kali baris pertama]

$\left[ \left.\begin{matrix} 1& 2& 3\\ 0& 1& -3\\ 0& -2& 5 \end{matrix}\right| \begin {array}{rrr} 1& 0& 0\\ -2& 1& 0\\ -1& 0& 1\end {array}\right]$
baris ketiga: B₃ + 2B₂ [artinya baris ketiga dijumlahkan dengan 2 kali baris kedua]

$\left[ \left.\begin{matrix} 1& 2& 3\\ 0& 1& -3\\ 0& 0& -1 \end{matrix}\right| \begin {array}{rrr} 1& 0& 0\\ -2& 1& 0\\ -5& 2& 1\end {array}\right]$
baris ketiga: B₃ x (-1) [artinya baris ketiga dikali dengan -1]

$\left[ \left.\begin{matrix} 1& 2& 3\\ 0& 1& -3\\ 0& 0& 1 \end{matrix}\right| \begin {array}{rrr} 1& 0& 0\\ -2& 1& 0\\ 5& -2& -1\end {array}\right]$
baris kedua : B₂ + 3B₃ [artinya baris kedua dijumlahkan dengan 3 kali baris ketiga]

baris pertama : B₁ + (-3B₃) [artinya baris pertama dijumlahkan dengan -3 kali baris ketiga]

$\left[ \left.\begin{matrix} 1& 2& 0\\ 0& 1& 0\\ 0& 0& 1 \end{matrix}\right| \begin {array}{rrr} -14& 6& 3\\ 13& -5& -3\\ 5& -2& -1\end {array}\right]$
baris pertama : B₁ + (-2B₂) [artinya baris pertama dijumlahkan dengan -2 kali baris kedua]

$\left [ \left.\begin{matrix} 1& 0& 0\\ 0& 1& 0\\ 0& 0& 1\end{matrix}\right|\begin{matrix} -40& 16& 9\\ 13& -5& -3\\ 5& -2& -1 \end{matrix} \right ]$

$\left[ \left.\begin{matrix} 1& 0& 0\\ 0& 1& 0\\ 0& 0& 1 \end{matrix}\right| \begin {array}{rrr} -40& 16& 9\\ 13& -5& -3\\ 5& -2& -1\end {array}\right]$

Karena matriks kiri sudah terbentuk menjadi matriks identitas, maka invers dari

matriks A adalah A^-1 = $\left [\begin{matrix} -40& 16& 9\\ 13& -5& -3\\ 5& -2& -1 \end{matrix} \right ]$

Contoh 3:

Periksa apakah matriks A_3×3 memiliki invers? Jika, tentukan inversnya, dengan A =

$\left [\begin{matrix} 3& 1& 5\\ 2& 4& 1\\ -4& 2& -9 \end{matrix} \right ]$ .

Penyelesaian:

Susun matriks sedemikian sehingga seperti dibawah ini, kemudian lakukan Operasi Baris Elementer

$\left [ \left.\begin{matrix} 3& 1& 5\\ 2& 4& 1\\ -4& 2& -9\end{matrix}\right|\begin{matrix} 1& 0& 0\\ 0& 1& 0\\ 0& 0& 1 \end{matrix} \right ]$

baris pertama : B₁ x (1/3)

$\left [ \left.\begin{matrix} 1& 1/3& 5/3\\ 2& 4& 1\\ -4& 2& -9\end{matrix}\right|\begin{matrix} 1/3& 0& 0\\ 0& 1& 0\\ 0& 0& 1 \end{matrix} \right ]$
baris kedua : B₂ + (-2B₁)

baris ketiga : B₃ + 4B₁

$\left [ \left.\begin{matrix} 1& 1/3& 5/3\\ 0& 10/3& -7/3\\ 0& 10/3& -7/3\end{matrix}\right|\begin{matrix} 1/3& 0& 0\\ -2/3& 1& 0\\ 4/3& 0& 1 \end{matrix} \right ]$

Perhatikan matriks sebebelah kiri pada baris kedua dan ketiga. Karena baris kedua dan ketiga memiliki entry yang sama, ini mengakibatkan matriks tersebut memiliki dterminannya nol, sehingga matriks tersebut tidak memiliki invers.

Silahkan download file pdf

Mat Eko_Stat Eko & Metrik

27 Agustus 2013