Sekilas Tentang Distribusi Poisson
Distribusi poisson (dalam wikipedia) diberi nama sesuai dengan penemunya yaitu Siméon-Denis Poisson (1781–1840), dilahirkan di Pithiers pada tanggal 21 Juni 1781. Poisson
terkenal karena penerapan ilmu matematikanya dalam mekanika dan fisika. Usaha
dan karya ilmiahnya ada di sekitar 300 sampai 400 buah. Tulisannya dalam Traité de mécanique, dipublikasikan
dalam dua volume pada tahun 1811 dan 1833, yang manjadi standar kerja dalam
mekanika dalam waktu yang lama. Salah satu teorinya yaitu Traité mathématique de la chaleur tahun 1835 ditambah sebuah
suplemen pada tahun 1837, dan karyanya yang lain adalah Recherches sur la probabilitié des jugements (1837). Recherches sur la probabilitié des
jugements merupakan sebuah karya penting dalam ilmu probabilitas yang
dipublikasikan pada tahun 1837, di tahun ini juga distribusi poisson pertama kali
muncul (http://wordpress/distribusi_poisson, 2010).
Distribusi ini merupakan distribusi probabilitas untuk variabel diskrit acak yang mempunyai nilai 0, 1, 2,
3 dan seterusnya. Suatu bentuk dari distribusi ini adalah rumus pendekatan
peluang poisson untuk peluang binomial yang dapat digunakan untuk pendekatan
probabilitas binomial dalam situasi tertentu (http://www.snapdrive.net,
2010).
Distribusi poisson dapat digunakan untuk menentukan probabilitas dari
sejumlah sukses yang ditentukan. Kejadian-kejadian terjadi dalam ruang
kontinyu. Proses poisson seperti proses Bernoulli, hanya berbeda pada sifat
kontinuitasnya saja (Haryono, 1994). Distribusi poisson banyak digunakan dalam hal berikut:
1. Menghitung probabilitas terjadinya peristiwa
menurut satuan waktu, ruang, luas, atau panjang tertentu, seperti menentukan
probabilitas dari:
a. Banyaknya penggunaan telepon per menit atau
banyaknya mobil yang lewat selama 5 menit di suatu ruas jalan.
b. Banyaknya bakteri dalam 1 tetes atau 1 liter
air.
c. Banyaknya kesalahan ketik per halaman sebuah
buku.
d. Banyaknya kecelakaan mobil di jalan tol
selama minggu pertama pada bulan April.
2. Menghitung distribusi binomial apabila nilai
n besar (n≥ 30) dan p kecil (p < 0,1).
Percobaan poisson adalah percobaan yang menghasilkan peubah acak X yang bernilai
numerik,yaitu banyaknya sukses selama selang waktu tertentu atau dalam daerah tertentu. Selang waktu
tertentu dapat berupa
sedetik, semenit, sejam, sehari, seminggu maupun
sebulan. Daerah tertentu dapat berupa satu meter,
satu kilometer persegi dan lain-lain. Distribusi peluang peubah acak poisson X, yang menyatakan banyaknya sukses yang terjadi dalam suatu selang waktu atau daerah
tertentu, diberikan oleh (http://kur2003.if.itb.ac.id,
2010):
Keterangan:
x
: 0,1,2, …
μ : Rata-rata banyaknya sukses.
e
: Bilangan alam (2,71828).
Pengertian Distribusi
Poisson
Distribusi peluang suatu peubah acak poisson
X disebut distribusi poisson dan dinyatakan dengan p(x;μ),
karena nilainya hanya tergantung
pada μ, yaitu rata-rata banyaknya sukses
yang terjadi pada selang waktu atau daerah
tertentu. Rataan dan variansi distribusi poisson p(x;
μ) keduanya
sama dengan μ. Berikut ini adalah penjelasan mengenai populasi (n) dan
peluang (p) pada distribusi poisson.
1.
Bila n
besar dan p dekat dengan nol, distribusi poisson
dapat digunakan, dengan μ
= np, untuk menghampiri
peluang binomial.
2.
Bila p
dekat dengan 1, distribusi poisson masih
dapat dipakai untuk menghampiri peluang
binomial dengan mempertukarkan apa yang
telah dinamai dengan sukses dan gagal, jadi
dengan mengganti p dengan suatu nilai yang
dekat dengan nol (http://kur2003.if.itb.ac.id, 2010).
Sebaran poisson dan binom memiliki histrogram yang bentuknya hampir sama
bila n besar dan p kecil (dekat dengan 0). Kedua kondisi
itu dipenuhi sebaran poisson dengan  = np dapat digunakan untuk menghampiri
peluang binom. P nilainya dekat
dengan 1 dapat saling menukarkan apa yang telah didefinisikan sebagai
keberhasilan dan kegagalan, dengan demikian mengubah p menjadi
suatu nilai yang dekat dengan 0
(Walpole, 1995).
= np dapat digunakan untuk menghampiri
peluang binom. P nilainya dekat
dengan 1 dapat saling menukarkan apa yang telah didefinisikan sebagai
keberhasilan dan kegagalan, dengan demikian mengubah p menjadi
suatu nilai yang dekat dengan 0
(Walpole, 1995).
Sifat
Percobaan
Poisson
Suatu percobaan yang dilakukan sebanyak N kali, menghasilkan peubah acak X,
misalkan banyaknya sukses selama selang waktu tertentu, dimana peluang yang sangat kecil (p mendekati 0), maka percobaan tersebut dinamakan poisson (http://elearning.gunadarma.ac.id,
2010). Beberapa sifat distribusi poisson adalah sebagai berikut
(http://kur2003.if.itb.ac.id,
2010):
1. Banyaknya
sukses terjadi dalam suatu selang waktu atau
daerah tertentu tidak terpengaruh oleh apa yang terjadi pada selang waktu atau
daerah lain yang dipilih (bebas).
2.
Peluang
terjadinya suatu sukses (tunggal) dalam selang
waktu yang amat pendek atau dalam daerah yang
kecil sebanding dengan panjang selang waktu atau besarnya daerah dan tidak tergantung pada banyaknya sukses yang terjadi di luar
selang waktu atau daerah tersebut.
3. Peluang terjadinya lebih dari satu sukses
dalam selang waktu yang pendek atau daerah yang
sempit tersebut dapat diabaikan.
Bilangan X yang menyatakan
banyaknya hasil percobaan dalam suatu percobaan poisson disebut peubah acak poisson dan sebaran peluangnya disebut sebaran
poisson, karena nilai-nialai peluangnya hanya bergantung pada  , yaitu rata-rata banyaknya hasil percobaan yang terjadi
selama selang waktu atau daerah yang diberikan (Walpole, 1995).
, yaitu rata-rata banyaknya hasil percobaan yang terjadi
selama selang waktu atau daerah yang diberikan (Walpole, 1995).
Pendekatan Peluang Poisson untuk Binomial
Pendekatan peluang poisson untuk peluang binomial dilakukan untuk
mendekatkan probabilitas-probabilitas dari kelas sukses (x) dari n percobaan
binomial dalam situasi dimana n sangat besar dan probabilitas kelas sukses (p)
sangat kecil. Aturan yang diikuti oleh kebanyakan ahli statistika adalah
bahwa n cukup besar dan p cukup kecil,
jika n adalah 20 atau lebihdari 20 dan p adalah 0,05 atau kurang dari 0,05.
Pendekatan ini rumusnya lebih mudah untuk digunakan dibandingkan dengan rumus binomial. Rumus
pendekatannya adalah (http://www.snapdrive.net, 2010):

Keterangan:
e : Bilangan alam (2,71828).
x : Banyaknya unsur
berhasil dalam sampel.
n : Jumlah data.
p : Probabilitas kelas sukses.
Peristiwa Kedatangan pada Distribusi Poisson
Suatu
proses atau peristiwa kedatangan yang terjadi dalam suatu interval waktu
tertentu dapat digolongkan sebagai proses keatangan poisson jika memenuhi
beberapa kriteria tertentu. Berikut ini adalah beberapa kriteria pada peristiwa
kedatangan dalam distribusi poisson (http://ma-dasar.gunadarma.ac.id/wp-content,
2010)
1.
Tingkat kedatangan rata-rata setiap unit
waktu adalah konstan.
2.
Jumlah kedatangan pada interval waktu tidak
bergantung pada apa yang terjadi di interval waktu yang sudah berlalu. Hal ini
memiliki makna bahwa kesempatan dari sebuah kedatangan di waktu berikutnya
adalah sama.
3.
Probabilitas untuk peristiwa lebih dari
satu kedatangan akan semakin mendekati nol jika interval semakin pendek. Misalnya,
jumlah pengunjung suatu restoran tidak mungkin lebih dari satu orang yang dapat
melalui pintu masuk dalam waktu satu detik.
Proses
perhitungan secara manual dapat digunakan untuk menentukan probabilitas suatu
kedatangan yang berdistribusi poisson. Perobabilitas kedatangan yang sesuai
dengan kriteria distribusi poisson dapat dihitung dengan menggunakan rumus
berikut:

Keterangan:
λ : Tingkat kedatangan rata-rata tiap unit
waktu.
t :
Jumlah unit waktu.


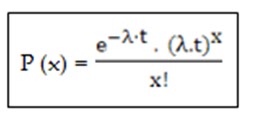















0 komentar:
Posting Komentar