Analisis regresi mempelajari bentuk hubungan antara satu atau lebih
peubah bebas (X) dengan satu peubah tak bebas (Y). dalam penelitian peubah
bebas ( X) biasanya peubah yang ditentukan oleh peneliti secara bebas misalnya
dosis obat, lama penyimpanan, kadar zat pengawet, umur ternak dan sebagainya.
Disamping itu peubah bebas bisa juga berupa peubah tak bebasnya, misalnya dalam
pengukuran panjang badan dan berat badan sapi, karena panjang badan lebih mudah
diukur maka panjang badan dimasukkan kedalam peubah bebas (X), sedangkan berat
badan dimasukkan peubah tak bebas (Y). sedangkan peubah tak bebas (Y) dalam
penelitian berupa respon yang diukur akibat perlakuan/peubah bebas (X).
misalnya jumlah sel darah merah akibat pengobatan dengan dosis tertentu, jumlah
mikroba daging setelah disimpan beberapa hari, berat ayam pada umur tertentu dan sebagainya.
Bentuk hubungan antara
peubah bebas (X) dengan peubah tak bebas (Y) bisa dalam bentuk polinom derajat
satu (linear) polinom derajat dua (kuadratik). Polinim derajat tiga (Kubik) dan
seterusnya. Disamping itu bisa juga dalam bentuk lain misalnya
eksponensial,logaritma,sigmoid dan sebagainya. Bentuk-bentuk ini dalam analisis
regresi-korelasi biasanya ditransformasi supaya menjadi bentuk polinom.
Dalam bentuk yang paling
sederhana yaitu satu peubah bebas (X) dengan satu peubah tak bebas (Y) mempunyai
persamaan :
Y =a +bx
Disini a disebut intersep dan b koefisien arah
Dalam pengertian fungsi
persamaan garis Y + a + bx hanya ada satu yang dapat dibentuk dari dua buah
titik dengan koordinat yang berbeda yaitu ( X1, Y1) dan X2,Y2).
Hal ini berarti kita bisa membuat banyak sekali persamaan garis dalam bentuk
lain melalui dua buat titik yang berbeda koordinatnya/tidak berimpit.
Persamaan
garis melalui dua buah titik dirumuskan sebagai berikut:
Sebagai contoh misalnya titik A (1,3) dan titik B ($,9) maka persamaan gais linear yang dapat dibuat adalah:
Dalam bentuk matrik bisa kita buat persaman sebagai berikut:
Jadi a=1 dan b=2 sehingga persamaannya Y=1 +2X
Jika jumlah data sebanyak n maka persamaannya sebagai berikut:
disini βo adalah penduga a, β1 adlah penduga b
dan εi merupakan besarnya simpangan persamaan garis penduga. Semakin
kecil nilai εi persamaan regresi yang diperoleh akan semakin baik.
Jadi kita dapat menuliskan pengamatan kita menjadi:
Dengan notasi matrik dapat ditulis sebagi berikut:
Jadi kita peroleh matrik Y,X,β dan ε dengan dimensi sebagi berikut :
Jika diasumsikan E(ε) = 0 maka E(Y) = Xβ
Bila modelnya benar β
merupakan enduga terbaik yaitu dengan jalan melakukan penggadaaan awal dengan
X’ sehingga diperoleh persamaan normal sebagai berikut:
Jadi β=(X’X)-1X’Y
Disini(X’X)-1 adalah kebalikan (inverse)dari matrik X’X
Contoh :
Seorang peneliti ingin
mengetahui bentuk hubungan antara jumlah cacing jenis tertentu denagn jumlah
telurnya pada usus ayam buras. Untuk tujuan tersebut diperiksa 20 ekor ayam dan
ditemukan sebagai berikut :
Tabel 1 jumlah cacing dan jumlah telurnya pada usus ayam buras am
buras.
No
|
Jumlah Cacing ( Xi)
|
Jumlah telurnya (Yi)
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
|
12
14
13
12
15
16
13
11
10
11
12
13
17
19
13
11
16
12
14
15
|
45
50
51
43
61
62
50
43
40
44
48
52
70
76
53
43
60
48
53
63
|
Total
|
269
|
1055
|
rataan
|
13,45
|
52,75
|
Dari data diatas kita bisa menghitung:
Bila kita duga bentuk hubungan antara jumlah cacing (X)dan jumlah
telurnya (Y) adalah:
Jadi Ŷ=-2,442 + 4,103 Xi + e
Persamaan garis regresi Yi =-2,442 + 4,103 Xi bukanlah satu-satunya
garis penduga untuk menyatakan hubungan antara jumlah cacing dengan jumlah
telurnya. Sudah barang tentu masih banyak lagi bentuk persamaan penduga yang
dapat dibuat misalnya dalam bentuk persamaan Yi=βo+β1Xi+β2Xi2,Yi=βoXiβ1
( dalam bentuk linear LnYi=Ln βo+βiLnXi) dan masih banyak
lagi bentuk yang lainnya
Untuk menyatakan apakah garis yang diperoleh
cukup baik untuk menggambarkan hubungan antara peubah bebas (X) dengan peubah
tak bebas(Y) dapat dilakukan pengujian bentuk model yang digunakan dan keeratan
hubungannya (korelasinya) untuk menyatakan ketepatan dan ketelitian persamaan
garis regresi yang diperoleh.


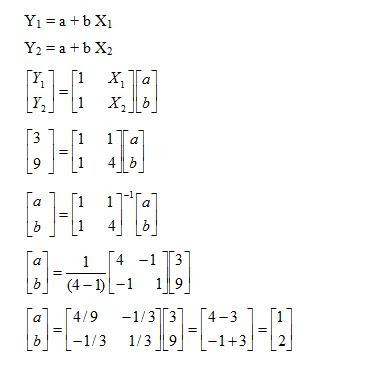

























0 komentar:
Posting Komentar