Suatu
matriks dapat dibalik jika dan hanya jika matriks tersebut adalah
matriks persegi (matriks yang berukuran n x n) dan matriks tersebut
non-singular (determinan 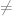 0). Tidak semua matriks memiliki invers. Invers matriks dapat didefinisikan sebagai berikut.
0). Tidak semua matriks memiliki invers. Invers matriks dapat didefinisikan sebagai berikut.
Contoh 1:
Contoh soal dari determinan ditunjukkan sebagai berikut:
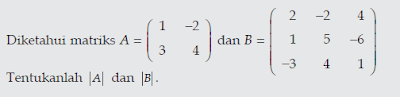
jawabannya...
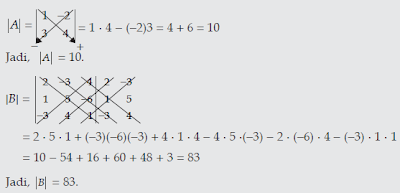
nah..untuk beberapa soal dan pembahasan UN, disajikan sebagai berikut ini...

jawaban dari soal diatas adalah,...
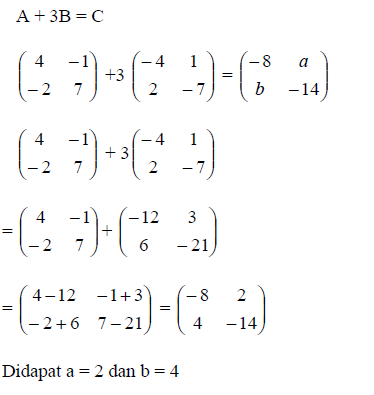
Untuk soal berikutnya, disajikan pada soal sebagai berikut

jawabannya adalah...
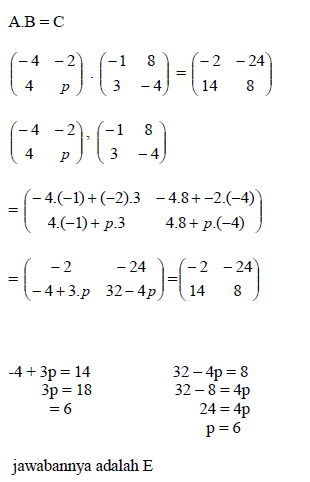
gimana gan???
masih kurang soalnya...
ini gua kasih lagi............ #logat jakarta..
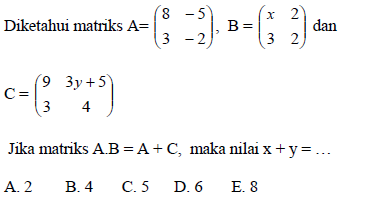
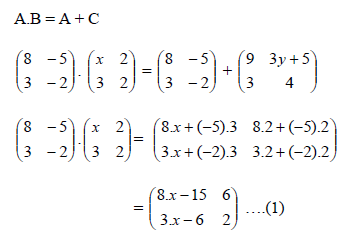
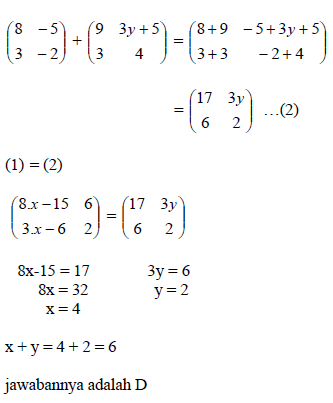
Definisi:
Jika
A adalah suatu matriks kuadrat, dan jika kita dapat mencari matriks B
sehingga AB = BA = I, maka A dikatakan dapat dibalik (invertible) dan B
dinamakan invers dari A
Sumber Lain:
Sifat matriks invers:
1.
(At)t = A
2.
(A + B)t = At + Bt
3.
(A . B)t = Bt . At
4.
(A-t)-t = A
5.
(A . B)-1 = B-1 . A-1
6.
A . B = C ® |A| . |B| = |C|
Sumber Lain:
For a 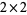 matrix
matrix
(2)
|
the matrix inverse is
(3)
| |||
(4)
|
Contoh 1:
Hitung invers matriks A2×2 berikut A = ![\left [ \begin{array}{rr}3 & 5\\ 1 & 2\end{array} \right ] \left [ \begin{array}{rr}3 & 5\\ 1 & 2\end{array} \right ]](http://s0.wp.com/latex.php?latex=%5Cleft+%5B+%5Cbegin%7Barray%7D%7Brr%7D3+%26+5%5C%5C+1+%26+2%5Cend%7Barray%7D+%5Cright+%5D&bg=ffffff&fg=666666&s=0) .
.
Penyelesaian:
Jika kita punya matriks 2×2, misal A = ![\left [ \begin{array}{rr}a & b\\ c & d\end{array} \right ] \left [ \begin{array}{rr}a & b\\ c & d\end{array} \right ]](http://s0.wp.com/latex.php?latex=%5Cleft+%5B+%5Cbegin%7Barray%7D%7Brr%7Da+%26+b%5C%5C+c+%26+d%5Cend%7Barray%7D+%5Cright+%5D&bg=ffffff&fg=666666&s=0) , maka invers matriks dapat dihitung menggunakan rumus
, maka invers matriks dapat dihitung menggunakan rumus
A-1 = B = 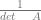
![\left [ \begin{array}{rr}d & -b\\ -c & a\end{array} \right ] \left [ \begin{array}{rr}d & -b\\ -c & a\end{array} \right ]](http://s0.wp.com/latex.php?latex=%5Cleft+%5B+%5Cbegin%7Barray%7D%7Brr%7Dd+%26+-b%5C%5C+-c+%26+a%5Cend%7Barray%7D+%5Cright+%5D&bg=ffffff&fg=666666&s=0)
= 
![\left [ \begin{array}{rr}2 & -5\\ -1 & 3\end{array} \right ] \left [ \begin{array}{rr}2 & -5\\ -1 & 3\end{array} \right ]](http://s0.wp.com/latex.php?latex=%5Cleft+%5B+%5Cbegin%7Barray%7D%7Brr%7D2+%26+-5%5C%5C+-1+%26+3%5Cend%7Barray%7D+%5Cright+%5D&bg=ffffff&fg=666666&s=0)
= ![\left [ \begin{array}{rr}2 & -5\\ -1 & 3\end{array} \right ] \left [ \begin{array}{rr}2 & -5\\ -1 & 3\end{array} \right ]](http://s0.wp.com/latex.php?latex=%5Cleft+%5B+%5Cbegin%7Barray%7D%7Brr%7D2+%26+-5%5C%5C+-1+%26+3%5Cend%7Barray%7D+%5Cright+%5D&bg=ffffff&fg=666666&s=0)
Cek, apakah AB = BA = I
AB = ![\left [ \begin{array}{rr}3 & 5\\ 1 & 2\end{array} \right ] \left [ \begin{array}{rr}3 & 5\\ 1 & 2\end{array} \right ]](http://s0.wp.com/latex.php?latex=%5Cleft+%5B+%5Cbegin%7Barray%7D%7Brr%7D3+%26+5%5C%5C+1+%26+2%5Cend%7Barray%7D+%5Cright+%5D&bg=ffffff&fg=666666&s=0)
![\left [ \begin{array}{rr}2 & -5\\ -1 & 3\end{array} \right ] \left [ \begin{array}{rr}2 & -5\\ -1 & 3\end{array} \right ]](http://s0.wp.com/latex.php?latex=%5Cleft+%5B+%5Cbegin%7Barray%7D%7Brr%7D2+%26+-5%5C%5C+-1+%26+3%5Cend%7Barray%7D+%5Cright+%5D&bg=ffffff&fg=666666&s=0) =
= ![\left [ \begin{array}{rr}1 & 0\\ 0 & 1\end{array} \right ] \left [ \begin{array}{rr}1 & 0\\ 0 & 1\end{array} \right ]](http://s0.wp.com/latex.php?latex=%5Cleft+%5B+%5Cbegin%7Barray%7D%7Brr%7D1+%26+0%5C%5C+0+%26+1%5Cend%7Barray%7D+%5Cright+%5D&bg=ffffff&fg=666666&s=0) = I
= I
BA = ![\left [ \begin{array}{rr}2 & -5\\ -1 & 3\end{array} \right ] \left [ \begin{array}{rr}2 & -5\\ -1 & 3\end{array} \right ]](http://s0.wp.com/latex.php?latex=%5Cleft+%5B+%5Cbegin%7Barray%7D%7Brr%7D2+%26+-5%5C%5C+-1+%26+3%5Cend%7Barray%7D+%5Cright+%5D&bg=ffffff&fg=666666&s=0)
![\left [ \begin{array}{rr}3 & 5\\ 1 & 2\end{array} \right ] \left [ \begin{array}{rr}3 & 5\\ 1 & 2\end{array} \right ]](http://s0.wp.com/latex.php?latex=%5Cleft+%5B+%5Cbegin%7Barray%7D%7Brr%7D3+%26+5%5C%5C+1+%26+2%5Cend%7Barray%7D+%5Cright+%5D&bg=ffffff&fg=666666&s=0) =
= ![\left [ \begin{array}{rr}1 & 0\\ 0 & 1\end{array} \right ] \left [ \begin{array}{rr}1 & 0\\ 0 & 1\end{array} \right ]](http://s0.wp.com/latex.php?latex=%5Cleft+%5B+%5Cbegin%7Barray%7D%7Brr%7D1+%26+0%5C%5C+0+%26+1%5Cend%7Barray%7D+%5Cright+%5D&bg=ffffff&fg=666666&s=0) = I
= I
Karena AB = BA = I, maka berdasarkan Definisi, B adalah invers dari matriks A.
Bagaimana
cara menghitung invers jika matriksnya memiliki ordo lebih dari 2?
Misal matriks 3×3, 4×4, dan seterusnya. Pada matriks yang berordo lebih
dari dua ini kita akan memanfatkan Eliminasi Gauss Jordan.
Sumber: Anton, H., 1992, Aljabar Linier Elementer, Erlangga, Jakarta.Contoh soal dari determinan ditunjukkan sebagai berikut:
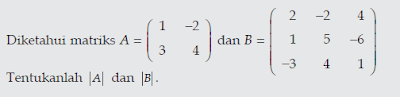
jawabannya...
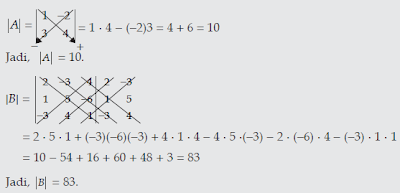
nah..untuk beberapa soal dan pembahasan UN, disajikan sebagai berikut ini...

jawaban dari soal diatas adalah,...
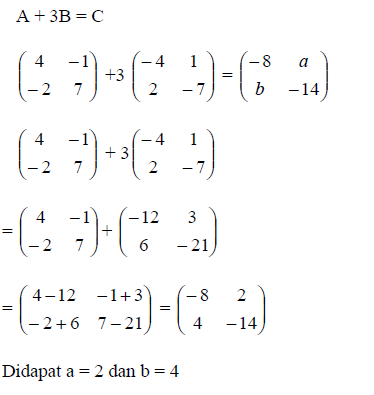
Untuk soal berikutnya, disajikan pada soal sebagai berikut

jawabannya adalah...
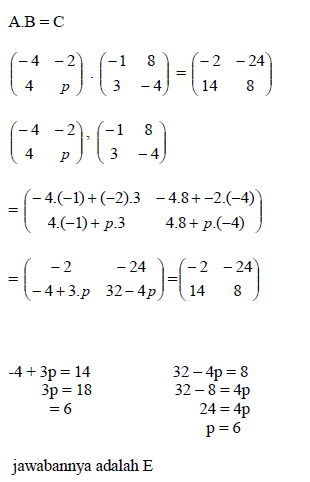
gimana gan???
masih kurang soalnya...
ini gua kasih lagi............ #logat jakarta..
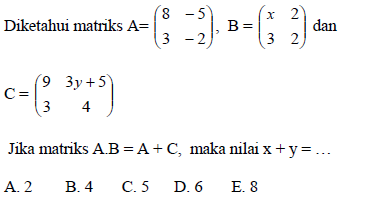
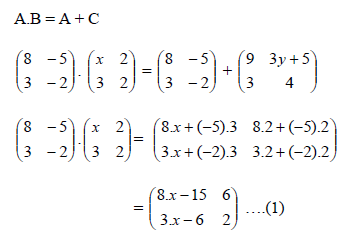
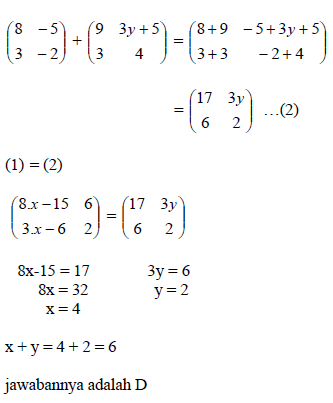















0 komentar:
Posting Komentar