DISTRIBUSI NORMAL
Distribusi normal, disebut pula distribusi Gauss, adalah distribusi probabilitas yang paling banyak digunakan dalam berbagai analisis statistika. Distribusi normal baku adalah distribusi normal yang memiliki rata-rata nol dan simpangan baku satu. Distribusi ini juga dijuluki kurva lonceng (bell curve) karena grafik fungsi kepekatan probabilitasnya mirip dengan bentuk lonceng.
Distribusi normal memodelkan fenomena kuantitatif pada ilmu alam maupun ilmu sosial. Beragam skor pengujian psikologi dan fenomena fisika seperti jumlah foton dapat dihitung melalui pendekatan dengan mengikuti distribusi normal. Distribusi normal banyak digunakan dalam berbagai bidang statistika, misalnya distribusi sampling rata-rata
akan mendekati normal, meski distribusi populasi yang diambil tidak
berdistribusi normal. Distribusi normal juga banyak digunakan dalam
berbagai distribusi dalam statistika, dan kebanyakan pengujian hipotesis mengasumsikan normalitas suatu data. (sumber : id.wikipedia.org/wiki/Distribusi_normal)
Kurva normal adalah bila X adalah suatu peupab acak normal dengan nilai tengah µ dan ragam σ2, maka persamaannya adalah
Untuk – ∞ < x < ∞. Dalam hal ini π = 3.14159… dan e = 2.71828…
Bentuk kurva normal itu sendiri berbeda tergantung dari nilai µ dan σ2
nya. Jika nilai µ berharga positif maka kurva akan bergeser ke kanan
dan jika bernilai negatif maka kurva akan bergeser ke kiri dari titik X = 0. Jika nilai σ2 bernilai semakin besar maka kurva normal akan semakin landai dan jika nilai σ2 bernilai semakin kecil maka kurva normal akan semakin curam. Berikut perbandingan kurvanya
Dari gambar di atas maka dapat diperoleh sifat-sifat kurva normal, yaitu :
- Modusnya yaitu titik pada sumbu mendatar yang membuat fungsi mencapai maksimum yang terjadi pada x = µ
- Kurvanya setangkup terhadapa suatu garis tegak yang melalui nilai tengah µ
- Kurva ini mendekati sumbu mendatar secara asimtotik dalam kedua arah bila kita semakin menjauhi nilai tengahnya.
- Luasan daerah yang terletak di bawah kurva tetapi di atas sumbu mendatar sama dengan 1
DISTRIBUSI BINOMIAL (1)
Dalam teori probabilitas dan statistika, distribusi binomial adalah distribusi probabilitas diskret jumlah keberhasilan dalam n percobaan ya/tidak (berhasil/gagal) yang saling bebas, dimana setiap hasil percobaan memiliki probabilitas p. Eksperimen berhasil/gagal juga disebut percobaan bernoulli. Ketika n = 1, distribusi binomial adalah distribusi bernoulli. Distribusi binomial merupakan dasar dari uji binomial dalam uji signifikansi statistik.
Distribusi ini seringkali digunakan untuk memodelkan jumlah keberhasilan pada jumlah sampel n dari jumlah populasi N. Apabila sampel tidak saling bebas (yakni pengambilan sampel tanpa pengembalian), distribusi yang dihasilkan adalah distribusi hipergeometrik, bukan binomial. Semakin besar N daripada n, distribusi binomial merupakan pendekatan yang baik dan banyak digunakan
Distribusi binomial juga didefinisikan bila suatu ulangan binomial mempunyai peluang keberhasilan p dan nilai peluang kegagalan a = 1 – p, maka sebaran peluang bagi peubah acak binomial X, yaitu banyaknya keberhasilan dalam n ulangan yang bebas adalah
untuk x = 0,1, 2, …, n
sedangkan untuk nilai tengah dan ragam bagi sebaran binomial adalah µ = np dan σ2 = npq. Hal ini dpat dibuktikan misalkan hasil pada ulangan ke-j dinyatakan oleh peubah acak Ij yang bernilai 0 dan 1, masing-masing dengan peluang q dan p. Ini disebur peubah Bernoulli atau lebih tepat disebut peubah indikator, Karena Ij = 0 berarti kegagalan dan Ij =
1 yang berarti keberhasilan. Dengan demiklian, dalam suatu percobaan
binomial banyaknya keberhasilan dapat dituliskan sebagai jumlah n peubah indikator yang bebas, sehingga
X = I1 + I2 + … + In
Nilai tengah Ij adalah E(Ij) = 0.q + 1.p = p. Maka kita mendapatkan nilai tengah bagi sebaran binomial, yaitu
µ = E(X) = E(X1) + E(X2) + … + E(Xn)
= p + p + … + p
= np
Ragam bagi setiap Ij adalah
σ2Ij = E[(Ij – p)2] = E(Ij2) – p2
= (0)2q + (1)2p – p2
= p(1 – p) = pq
Dengan demikian, ragam sebaran binomial adalah
σ2x = σ2I1 + σ2I2 + … + σ2In
= pq + pq + … + pq
= npq
Distribusi Binomial (2)
Suatu percobaan sering kali terdiri atas
ulangan-ulangan, dan masing-masin mempuyai dua kemungkinan hasil yang
dapat diberi nama berhasil dan gagal. Misalnya saja dalam pelemparan
sekeping uang logam sebanyak 5 kali. Hasil setiap ulangan mungkin muncul
sisi gambar atau sisi angka. Dan salah satu diantara keduanya
ditentukan sebagai “berhasil”. Begitupula, bila 5 kartu diambil
berturut-turut. Untuk kartu merah diberi label “berhasil” atau “gagal”
jika yang terambil warna hitam.
Bila setiap kartu dikembalikan
sebelum pengembalian berikutnya, maka kedua percobaan yan dilakukan
diatas mempunyai ciri-ciri sama, yaitu bahwa ulangan-ulangan tersebut
bersifat bebas dan peluang keberhasilan setiap ulangan tetap sama yaitu
sebesar ½. Percobaan semacam ini dinamakan percobaaan binom. Perhatikan
bahwa dalam percobaan pengambilan kartu tersebut, peluang keberhasilan
dalam setiap ulangan akan berubah ila kartu tidak dikebalikan sebelum
pengambilan berikutnya. Karena peluang terambilnya pada pengambilan
pertama adalah ½, sedangkan pada engambila yang kedua peluang itu
bersifat bersyarat, bernilai 26/51 atau 25/51, bergantung pada hasil
pengembalian pertama. Bila demikian halnya percobaan ini bukan bersifat
binom. Untuk lebih ringkasnya dapat dilihat pada definisi berikut.
Jika
suatu ulangan binomial mempunyai peluang keberhasilan p dan peluang
kegagala q=1-p , maka distribusi probabilitas bagi peubah acak binomial
x, yaitu banyaknya keberhasilan dalam n ulangn bebas , adalah
B(x;n;p) = Cxn px qn-x
Untuk x=1,2,3,4,……., n
Contoh :
Tentukan peluang mendapatkan tepat tiga bilangan 2 buah dadu setimbang dilempar 5 kali.
Jawab
: peluang keberhasilan setiap ulangan yang bebas ini adalah 1/6 dan
peluang kegagalan adalah 5/6. Dalam hal itu munculnya bilangan 2 di
anggap keberhasilan. Maka :
B {x;5,1/6} = C35 (1/6)3 (5/6)2
= 5! . 52 .
3! 2! 63
= 0,0032
Distribusi Multinomial
Percobaan
Binomial menjadi suatu percobaan multinomial bila kita membuat setiap
percobaan mempunyai lebih dari 2 keluaran yang mungkin. Penarikan sebuah
kartu dari suatu tumpukan dengan pengembalian merupakan percobaan
multinomial bila ke-empat jenis kartu menjadi keluarannya.
Secara
umum, Bila suatu percobaan dapat menghasilkan salah satu dari k keluaran
yan mungkin E1,E2, ………, Ek dengan probabilitas P1,P2, ………, Pk maka
sebaran probabilitaspeubah acak X1,X2, ……….., Xk yang mewakili jumlah
kejadian untuk E1,E2, ………, Ek didalam n percobaan yang bebas adalah
n X1 X2 ……X3
f(X1,X2,…….xk;P1,P2,…….Pk,n)= X1,X2,….XK P1 P2 PK
Dengan
∑ Xi = n dan ∑ Pi = 1
Contoh : Bila sepasang dadu dilemparkan 6 kali, berapakah probabilitas mendapatkan suatu total 7 atau 11 ebanyak 2 kali , pasangan angka yang sama sekali, dan sembarang gabungan lainnya sebanyak 3 kali.
Jawab : Kita daftar kejadian-kejadian yang mungkin berikut ini :
E1= sebuah total 7 atau 11 muncul
E2 = Pasangan angka yang sama muncul
E3 = Bukan angka sama atau bukan total 7 atau 11 yang muncul
Probabilitas
yang berkesuaian untuk percobaan yang diketahui tersebut adalah p1 =
2/9 , p2= 1/6 dan p3 = 11/18. Nilai-nilia in tetap konstan untuk ke 6
percobaan tersebut. Dengan menggunakan sebaran multinomial dengan x1 = 2
, x2 = 1, dan x3=3 kita dapatkan bahwa probabilitas yang diperlukan
adalah
Distribusi Hipergeometrik
Bila
dalam populasi N benda, k benfda diantaranya diberi label ‘berhasil’
N-k benda lainya diberi label ‘gagal’, maka distribusi probabilitas bagi
peubah acak geometrik X, yang menyatakan banyaknya keberhasilan dalam
contoh acak berukuran n, adalah
h(x;N,n,k) = .
Untuk x = 0,1,2,3, ………., k
Contoh :
Bila 5 kartu diambil secara acak dari seperankat kartu bridge, berapa probabilitas diperoleh 3 kartu hati.
Jawab : Dengan menggunakan sebaran hipergeometrik untuk n= 5, N=52 , k=13, dan x=3, maka probabilitas memperoleh 3 kartu hati adalah,
h(3;52,5,13)= ¬¬¬¬¬¬¬¬¬¬¬¬¬¬¬¬¬¬¬¬¬¬¬______________
sedangkan nilai rata-rata dan ragam bagi distribusi hipergeometrik h(x;N,n,k) adalah
μ = n k .
N
σ2 = N –n . n k . { 1 - k .}
N – 1 N N
Contoh : Dari contoh di atas tentukan μ dan σ2 nya
Jawab :
μ = (5) (13) . =1.25
52
σ2 = (47/51)(5)(13/52)(1-13/42)
Distribusi ini merupakan distribusi probabilitas untuk variabel diskrit acak yang mempunyai nilai 0, 1, 2, 3 dan seterusnya. Suatu bentuk dari distribusi ini adalah rumus pendekatan peluang poisson untuk peluang binomial yang dapat digunakan untuk pendekatan probabilitas binomial dalam situasi tertentu (http://www.snapdrive.net, 2010).
Distribusi poisson dapat digunakan untuk menentukan probabilitas dari
sejumlah sukses yang ditentukan. Kejadian-kejadian terjadi dalam ruang
kontinyu. Proses poisson seperti proses Bernoulli, hanya berbeda pada sifat
kontinuitasnya saja (Haryono, 1994). Distribusi poisson banyak digunakan dalam hal berikut:
1. Menghitung probabilitas terjadinya peristiwa
menurut satuan waktu, ruang, luas, atau panjang tertentu, seperti menentukan
probabilitas dari:
a. Banyaknya penggunaan telepon per menit atau
banyaknya mobil yang lewat selama 5 menit di suatu ruas jalan.
b. Banyaknya bakteri dalam 1 tetes atau 1 liter
air.
c. Banyaknya kesalahan ketik per halaman sebuah
buku.
d. Banyaknya kecelakaan mobil di jalan tol
selama minggu pertama pada bulan April.
2. Menghitung distribusi binomial apabila nilai
n besar (n≥ 30) dan p kecil (p < 0,1).
Percobaan poisson adalah percobaan yang menghasilkan peubah acak X yang bernilai
numerik,yaitu banyaknya sukses selama selang waktu tertentu atau dalam daerah tertentu. Selang waktu
tertentu dapat berupa
sedetik, semenit, sejam, sehari, seminggu maupun
sebulan. Daerah tertentu dapat berupa satu meter,
satu kilometer persegi dan lain-lain. Distribusi peluang peubah acak poisson X, yang menyatakan banyaknya sukses yang terjadi dalam suatu selang waktu atau daerah
tertentu, diberikan oleh (http://kur2003.if.itb.ac.id,
2010):
x
: 0,1,2, …
μ : Rata-rata banyaknya sukses.
e
: Bilangan alam (2,71828).
Pengertian Distribusi
Poisson
Distribusi peluang suatu peubah acak poisson
X disebut distribusi poisson dan dinyatakan dengan p(x;μ),
karena nilainya hanya tergantung
pada μ, yaitu rata-rata banyaknya sukses
yang terjadi pada selang waktu atau daerah
tertentu. Rataan dan variansi distribusi poisson p(x;
μ) keduanya
sama dengan μ. Berikut ini adalah penjelasan mengenai populasi (n) dan
peluang (p) pada distribusi poisson.
1.
Bila n
besar dan p dekat dengan nol, distribusi poisson
dapat digunakan, dengan μ
= np, untuk menghampiri
peluang binomial.
2.
Bila p
dekat dengan 1, distribusi poisson masih
dapat dipakai untuk menghampiri peluang
binomial dengan mempertukarkan apa yang
telah dinamai dengan sukses dan gagal, jadi
dengan mengganti p dengan suatu nilai yang
dekat dengan nol (http://kur2003.if.itb.ac.id, 2010).
Sebaran poisson dan binom memiliki histrogram yang bentuknya hampir sama
bila n besar dan p kecil (dekat dengan 0). Kedua kondisi
itu dipenuhi sebaran poisson dengan  = np dapat digunakan untuk menghampiri
peluang binom. P nilainya dekat
dengan 1 dapat saling menukarkan apa yang telah didefinisikan sebagai
keberhasilan dan kegagalan, dengan demikian mengubah p menjadi
suatu nilai yang dekat dengan 0
(Walpole, 1995).
= np dapat digunakan untuk menghampiri
peluang binom. P nilainya dekat
dengan 1 dapat saling menukarkan apa yang telah didefinisikan sebagai
keberhasilan dan kegagalan, dengan demikian mengubah p menjadi
suatu nilai yang dekat dengan 0
(Walpole, 1995).
Sifat
Percobaan
Poisson
Suatu percobaan yang dilakukan sebanyak N kali, menghasilkan peubah acak X, misalkan banyaknya sukses selama selang waktu tertentu, dimana peluang yang sangat kecil (p mendekati 0), maka percobaan tersebut dinamakan poisson (http://elearning.gunadarma.ac.id, 2010). Beberapa sifat distribusi poisson adalah sebagai berikut (http://kur2003.if.itb.ac.id, 2010):
Suatu percobaan yang dilakukan sebanyak N kali, menghasilkan peubah acak X, misalkan banyaknya sukses selama selang waktu tertentu, dimana peluang yang sangat kecil (p mendekati 0), maka percobaan tersebut dinamakan poisson (http://elearning.gunadarma.ac.id, 2010). Beberapa sifat distribusi poisson adalah sebagai berikut (http://kur2003.if.itb.ac.id, 2010):
1. Banyaknya
sukses terjadi dalam suatu selang waktu atau
daerah tertentu tidak terpengaruh oleh apa yang terjadi pada selang waktu atau
daerah lain yang dipilih (bebas).
2.
Peluang
terjadinya suatu sukses (tunggal) dalam selang
waktu yang amat pendek atau dalam daerah yang
kecil sebanding dengan panjang selang waktu atau besarnya daerah dan tidak tergantung pada banyaknya sukses yang terjadi di luar
selang waktu atau daerah tersebut.
3. Peluang terjadinya lebih dari satu sukses
dalam selang waktu yang pendek atau daerah yang
sempit tersebut dapat diabaikan.
Bilangan X yang menyatakan
banyaknya hasil percobaan dalam suatu percobaan poisson disebut peubah acak poisson dan sebaran peluangnya disebut sebaran
poisson, karena nilai-nialai peluangnya hanya bergantung pada  , yaitu rata-rata banyaknya hasil percobaan yang terjadi
selama selang waktu atau daerah yang diberikan (Walpole, 1995).
, yaitu rata-rata banyaknya hasil percobaan yang terjadi
selama selang waktu atau daerah yang diberikan (Walpole, 1995).
Pendekatan Peluang Poisson untuk Binomial
Pendekatan peluang poisson untuk peluang binomial dilakukan untuk
mendekatkan probabilitas-probabilitas dari kelas sukses (x) dari n percobaan
binomial dalam situasi dimana n sangat besar dan probabilitas kelas sukses (p)
sangat kecil. Aturan yang diikuti oleh kebanyakan ahli statistika adalah
bahwa n cukup besar dan p cukup kecil,
jika n adalah 20 atau lebihdari 20 dan p adalah 0,05 atau kurang dari 0,05.
Pendekatan ini rumusnya lebih mudah untuk digunakan dibandingkan dengan rumus binomial. Rumus
pendekatannya adalah (http://www.snapdrive.net, 2010):

Keterangan:
e : Bilangan alam (2,71828).
x : Banyaknya unsur
berhasil dalam sampel.
n : Jumlah data.
p : Probabilitas kelas sukses.
Peristiwa Kedatangan pada Distribusi Poisson
Suatu
proses atau peristiwa kedatangan yang terjadi dalam suatu interval waktu
tertentu dapat digolongkan sebagai proses keatangan poisson jika memenuhi
beberapa kriteria tertentu. Berikut ini adalah beberapa kriteria pada peristiwa
kedatangan dalam distribusi poisson (http://ma-dasar.gunadarma.ac.id/wp-content,
2010)
1.
Tingkat kedatangan rata-rata setiap unit
waktu adalah konstan.
2.
Jumlah kedatangan pada interval waktu tidak
bergantung pada apa yang terjadi di interval waktu yang sudah berlalu. Hal ini
memiliki makna bahwa kesempatan dari sebuah kedatangan di waktu berikutnya
adalah sama.
3. Probabilitas untuk peristiwa lebih dari
satu kedatangan akan semakin mendekati nol jika interval semakin pendek. Misalnya,
jumlah pengunjung suatu restoran tidak mungkin lebih dari satu orang yang dapat
melalui pintu masuk dalam waktu satu detik.
Proses perhitungan secara manual dapat digunakan untuk menentukan probabilitas suatu kedatangan yang berdistribusi poisson. Perobabilitas kedatangan yang sesuai dengan kriteria distribusi poisson dapat dihitung dengan menggunakan rumus berikut:
Proses perhitungan secara manual dapat digunakan untuk menentukan probabilitas suatu kedatangan yang berdistribusi poisson. Perobabilitas kedatangan yang sesuai dengan kriteria distribusi poisson dapat dihitung dengan menggunakan rumus berikut:

Keterangan:
λ : Tingkat kedatangan rata-rata tiap unit
waktu.
t :
Jumlah unit waktu.
x :
Jumlah kedatangan dalam t unit waktu.
Sumber:


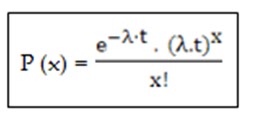












0 komentar:
Posting Komentar