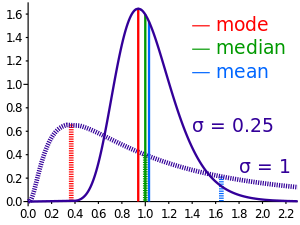
Jenis-Jenis Nilai Sentral
1. Rata -rata hitung ( mean )
Mean adalah nilai rata-rata dari beberapa buah data. Nilai mean dapat ditentukan dengan membagi jumlah data dengan banyaknya data.
Mean (rata-rata) merupakan suatu ukuran pemusatan data. Mean suatu data juga merupakan statistik karena mampu menggambarkan bahwa data tersebut berada pada kisaran mean data tersebut. Mean tidak dapat digunakan sebagai ukuran pemusatan untuk jenis data nominal dan ordinal.
Berdasarkan definisi dari mean adalah jumlah seluruh data dibagi dengan banyaknya data. Dengan kata lain jika kita memiliki N data sebagai berikut maka mean data tersebut dapat kita tuliskan sebagai berikut:

Dimana:
x = data ke n
x bar = x rata-rata = nilai rata-rata sampel
n = banyaknya data
Bisa juga Menghitung mean
a) Rumus Mean Hitung dari Data Tunggal

b) Rumus Mean Hitung Untuk Data yang Disajikan Dalam Distribusi Frekuensi
Dengan : fixi = frekuensi untuk nilai xi yang bersesuaian
xi = data ke-i
c) Rumus Mean Hitung Gabungan
2. Median
Median menentukan letak tengah data setelah data disusun menurut urutan nilainya. Bisa juga nilai tengah dari data-data yang terurut. Simbol untuk median adalah Me. Dengan median Me, maka 50% dari banyak data nilainya paling tinggi sama dengan Me, dan 50% dari banyak data nilainya paling rendah sama dengan Me. Dalam mencari median, dibedakan untuk banyak data ganjil dan banyak data genap. Untuk banyak data ganjil, setelah data disusun menurut nilainya, maka median Me adalah data yang terletak tepat di tengah. Median bisa dihitung menggunakan rumus sebagai berikut:
variansi merupakan salah satu ukuran sebaran yang paling sering digunakan dalam berbagai analisis statistika. Standar deviasi merupakan akar kuadrat positif dari variansi. Secara umum, variansi dirumuskun sabagai:
Contoh:
Dari lima kali kuiz statistika, seorang mahasiswa memperoleh nilai 82, 93, 86, 92, dan 79. Tentukan median populasi ini.
jawab:Setelah data disusun dari yang terkecil sampai terbesar, diperoleh 79 82 86 92 93
Oleh karena itu medianya adalah 86
Kadar nikotin yang berasal dari sebuah contoh acak enam batang rokok cap tertentu adalah 2.3, 2.7, 2.5, 2.9, 3.1, dan 1.9 miligram. Tentukan mediannya.
jawab:
Bila kadar nikotin itu diurutkan dari yang terkecil sampai terbesar, maka diperoleh 1.9 2.3 2.5 2.7 2.9 3.1
Maka mediannya adalah rata-rata dari 2.5 dan 2.7, yaitu

Selain itu juga dapat dicari median dari data yang telah tersusun dalam bentuk distribusi frekuensi. Rumus yang digunakan ada dua, yaitu:

Dimana :
Bak = batas kelas atas median
c = lebar kelas
s’ = selisih antara nomor frekuensi median dengan frekuensi kumulatif sampai kelas median
fM = frekuensi kelas median
Sebelum menggunakan kedua rumus di atas, terlebih dahulu harus ditentukan kelas yang menjadi kelas median. Kelas median adalah kelas yang memuat nomor frekuensi median, dan nomor frekuensi median ini ditentukan dengan membagi keseluruhan data dengan dua.
Secara singkat rumus median dapat digunakan sebagai berikut dalam perhitungan menggunakan tabel data
Mean (rata-rata) merupakan suatu ukuran pemusatan data. Mean suatu data juga merupakan statistik karena mampu menggambarkan bahwa data tersebut berada pada kisaran mean data tersebut. Mean tidak dapat digunakan sebagai ukuran pemusatan untuk jenis data nominal dan ordinal.
Berdasarkan definisi dari mean adalah jumlah seluruh data dibagi dengan banyaknya data. Dengan kata lain jika kita memiliki N data sebagai berikut maka mean data tersebut dapat kita tuliskan sebagai berikut:
Dimana:
x = data ke n
x bar = x rata-rata = nilai rata-rata sampel
n = banyaknya data
Bisa juga Menghitung mean
a) Rumus Mean Hitung dari Data Tunggal
b) Rumus Mean Hitung Untuk Data yang Disajikan Dalam Distribusi Frekuensi
Dengan : fixi = frekuensi untuk nilai xi yang bersesuaian
xi = data ke-i
c) Rumus Mean Hitung Gabungan
2. Median
Median menentukan letak tengah data setelah data disusun menurut urutan nilainya. Bisa juga nilai tengah dari data-data yang terurut. Simbol untuk median adalah Me. Dengan median Me, maka 50% dari banyak data nilainya paling tinggi sama dengan Me, dan 50% dari banyak data nilainya paling rendah sama dengan Me. Dalam mencari median, dibedakan untuk banyak data ganjil dan banyak data genap. Untuk banyak data ganjil, setelah data disusun menurut nilainya, maka median Me adalah data yang terletak tepat di tengah. Median bisa dihitung menggunakan rumus sebagai berikut:
variansi merupakan salah satu ukuran sebaran yang paling sering digunakan dalam berbagai analisis statistika. Standar deviasi merupakan akar kuadrat positif dari variansi. Secara umum, variansi dirumuskun sabagai:
Contoh:
Dari lima kali kuiz statistika, seorang mahasiswa memperoleh nilai 82, 93, 86, 92, dan 79. Tentukan median populasi ini.
jawab:Setelah data disusun dari yang terkecil sampai terbesar, diperoleh 79 82 86 92 93
Oleh karena itu medianya adalah 86
Kadar nikotin yang berasal dari sebuah contoh acak enam batang rokok cap tertentu adalah 2.3, 2.7, 2.5, 2.9, 3.1, dan 1.9 miligram. Tentukan mediannya.
jawab:
Bila kadar nikotin itu diurutkan dari yang terkecil sampai terbesar, maka diperoleh 1.9 2.3 2.5 2.7 2.9 3.1
Maka mediannya adalah rata-rata dari 2.5 dan 2.7, yaitu
Selain itu juga dapat dicari median dari data yang telah tersusun dalam bentuk distribusi frekuensi. Rumus yang digunakan ada dua, yaitu:
Dimana :
Bak = batas kelas atas median
c = lebar kelas
s’ = selisih antara nomor frekuensi median dengan frekuensi kumulatif sampai kelas median
fM = frekuensi kelas median
Sebelum menggunakan kedua rumus di atas, terlebih dahulu harus ditentukan kelas yang menjadi kelas median. Kelas median adalah kelas yang memuat nomor frekuensi median, dan nomor frekuensi median ini ditentukan dengan membagi keseluruhan data dengan dua.
Secara singkat rumus median dapat digunakan sebagai berikut dalam perhitungan menggunakan tabel data
Keterangan:
Md : Nilai Median
L : Tepi bawah dari kelas yang mengandung median
n : Jumlah data
fc : frekuensi komulatif pada kelas sebelum kelas median
fm : frekuensi (absolut) dari kelas terdapatnya median
C : Kelas interval
3. Modus
Modus adalah nilai yang sering muncul. Jika kita tertarik pada data frekuensi, jumlah dari suatu nilai dari kumpulan data, maka kita menggunakan modus. Modus sangat baik bila digunakan untuk data yang memiliki sekala kategorik yaitu nominal atau ordinal.
Sedangkan data ordinal adalah data kategorik yang bisa diurutkan, misalnya kita menanyakan kepada 100 orang tentang kebiasaan untuk mencuci kaki sebelum tidur, dengan pilihan jawaban: selalu (5), sering (4), kadang-kadang(3), jarang (2), tidak pernah (1). Apabila kita ingin melihat ukuran pemusatannya lebih baik menggunakan modus yaitu yaitu jawaban yang paling banyak dipilih, misalnya sering (2). Berarti sebagian besar orang dari 100 orang yang ditanyakan menjawab sering mencuci kaki sebelum tidur. Inilah cara menghitung modus:
- Data yang belum dikelompokkan
Modus dari data yang belum dikelompokkan adalah ukuran yang memiliki frekuensi tertinggi. Modus dilambangkan mo. - Data yang telah dikelompokkan
Rumus Modus dari data yang telah dikelompokkan dihitung dengan rumus:
Dengan : Mo = Modus
L = Tepi bawah kelas yang memiliki frekuensi tertinggi (kelas modus) i = Interval kelas
b1 = Frekuensi kelas modus dikurangi frekuensi kelas interval terdekat sebelumnya
b2 = frekuensi kelas modus dikurangi frekuensi kelas interval terdekat sesudahnya
Contoh:
Sumbangan dari warga Bogor pada hari Palang Merah Nasional tercatat sebagai berikut: Rp 9.000, Rp 10.000, Rp 5.000, Rp 9.000, Rp 9.000, Rp 7.000, Rp 8.000, Rp 6.000, Rp 10.000, Rp 11.000. Maka modusnya, yaitu nilai yang terjadi dengan frekuensi paling tinggi, adalah Rp 9.000.
Dari dua belas pelajar sekolah lanjutan tingkat atas yang diambil secara acak dicatat berapa kali mereka menonton film selama sebulan lalu. Data yang diperoleh adalah 2, 0, 3, 1, 2, 4, 2, 5, 4, 0, 1 dan 4. Dalam kasus ini terdapat dua modu, yaitu 2 dan 4, karena 2 dan 4 terdapat dengan frekuensi tertinggi. Distribusi demikian dikatakan bimodus.
Standar Deviasi
Standar Deviasi dan Varians Salah satu teknik statistik yg digunakan untuk menjelaskan homogenitas kelompok. Varians merupakan jumlah kuadrat semua deviasi nilai-nilai individual thd rata-rata kelompok. Sedangkan akar dari varians disebut dengan standar deviasi atau simpangan baku.
Standar Deviasi dan Varians Simpangan baku merupakan variasi sebaran
data. Semakin kecil nilai sebarannya berarti variasi nilai data makin
sama Jika sebarannya bernilai 0, maka nilai semua datanya adalah sama.
Semakin besar nilai sebarannya berarti data semakin bervariasi.
Cara penulisan rumus fungsi standar deviasi:
STDEV (number1, number2,…)
Dengan:
Number1, number2, … adalah 1-255 argumen yang sesuai dengan sampel populasi. Anda juga dapat menggunakan array tunggal atau referensi ke array, bukan argumen yang dipisahkan oleh koma.
Keterangan
a. STDEV mengasumsikan bahwa argumen adalah contoh dari populasi. Jika data anda mewakili seluruh populasi, untuk menghitung deviasi standar menggunakan STDEVP.
b. Standar deviasi dihitung menggunakan metode “n-1″ .
c. Argumen dapat berupa nomor atau nama, array, atau referensi yang mengandung angka.
d. Nilai-nilai logis dan representasi teks dari nomor yang Anda ketik langsung ke daftar argumen akan dihitung.
e. Jika argumen adalah sebuah array atau referensi, hanya nomor/angka dalam array atau referensi yang akan dihitung. Sel kosong, nilai-nilai logis, teks, atau nilai-nilai kesalahan dalam array atau referensi akan diabaikan.
f. Argumen yang kesalahan nilai atau teks yang tidak dapat diterjemahkan ke dalam nomor/angka akan menyebabkan kesalahan. g. Jika Anda ingin memasukkan nilai-nilai logis dan representasi teks angka dalam referensi sebagai bagian dari perhitungan, gunakan fungsi STDEVA.
Dalam penerapannya STDEV , perhitungan standar deviasi secara manual menggunakan rumus berikut:

Dimana:
x = data ke n
x bar = x rata-rata = nilai rata-rata sampel
n = banyaknya data
variansi merupakan salah satu ukuran sebaran yang paling sering digunakan dalam berbagai analisis statistika. Standar deviasi merupakan akar kuadrat positif dari variansi. Secara umum, variansi dirumuskun sabagai :
Jika kita memiliki n observasi yaitu X1,X2,….Xn, dan diketahui Xbar adalah rata-rata sampel yang dimiliki, maka variansi dapat dihitung sebagai:

Contoh:
Jika dimiliki data : 210, 340, 525, 450, 275
maka variansi dan standar deviasinya :
mean = (210, 340, 525, 450, 275)/5 = 360
variansi dan standar deviasi berturut-turut:

Sedangkan jika data disajikan dalam tabel distribusi frekuensi, variansi sampel dapat dihitung sebagai:

Cara penulisan rumus fungsi standar deviasi:
STDEV (number1, number2,…)
Dengan:
Number1, number2, … adalah 1-255 argumen yang sesuai dengan sampel populasi. Anda juga dapat menggunakan array tunggal atau referensi ke array, bukan argumen yang dipisahkan oleh koma.
Keterangan
a. STDEV mengasumsikan bahwa argumen adalah contoh dari populasi. Jika data anda mewakili seluruh populasi, untuk menghitung deviasi standar menggunakan STDEVP.
b. Standar deviasi dihitung menggunakan metode “n-1″ .
c. Argumen dapat berupa nomor atau nama, array, atau referensi yang mengandung angka.
d. Nilai-nilai logis dan representasi teks dari nomor yang Anda ketik langsung ke daftar argumen akan dihitung.
e. Jika argumen adalah sebuah array atau referensi, hanya nomor/angka dalam array atau referensi yang akan dihitung. Sel kosong, nilai-nilai logis, teks, atau nilai-nilai kesalahan dalam array atau referensi akan diabaikan.
f. Argumen yang kesalahan nilai atau teks yang tidak dapat diterjemahkan ke dalam nomor/angka akan menyebabkan kesalahan. g. Jika Anda ingin memasukkan nilai-nilai logis dan representasi teks angka dalam referensi sebagai bagian dari perhitungan, gunakan fungsi STDEVA.
Dalam penerapannya STDEV , perhitungan standar deviasi secara manual menggunakan rumus berikut:
Dimana:
x = data ke n
x bar = x rata-rata = nilai rata-rata sampel
n = banyaknya data
variansi merupakan salah satu ukuran sebaran yang paling sering digunakan dalam berbagai analisis statistika. Standar deviasi merupakan akar kuadrat positif dari variansi. Secara umum, variansi dirumuskun sabagai :
Jika kita memiliki n observasi yaitu X1,X2,….Xn, dan diketahui Xbar adalah rata-rata sampel yang dimiliki, maka variansi dapat dihitung sebagai:
Contoh:
Jika dimiliki data : 210, 340, 525, 450, 275
maka variansi dan standar deviasinya :
mean = (210, 340, 525, 450, 275)/5 = 360
variansi dan standar deviasi berturut-turut:
Sedangkan jika data disajikan dalam tabel distribusi frekuensi, variansi sampel dapat dihitung sebagai:













0 komentar:
Posting Komentar